What is it that feeds our battle, yet starves our victory?
This post is scheduled to go “live” at 10:01PM MST on Friday, December 20, 2024. That’s 00:01 EST on Saturday, December 21, 2024 for those of you in that benighted timezone near the Atlantic Ocean.
As of that moment, there are 30 days, 11 hours, and 59 minutes until our rightful President of the United States is restored to office.
Not that I’m counting, mind you.
January 6 Tapes Reminder
OK…I’m sick and tired of reminding you to no effect, Speaker Johnson, so I’ll do the more emotionally satisfying thing and call you a cowardly, lying, fraudulent sack of diarrhetic monkey shit.
Johnson, you are a cowardly, lying, fraudulent sack of diarrhetic monkey shit!
A Caution
Just remember…we might replace the RINO candidates. (Or we might not. The record is mixed even though there is more MAGA than there used to be.) But that will make no difference in the long run if the party officials, basically the Rhonna McDaniels (or however that’s spelled–I suspect it’s RINO), don’t get replaced.
State party chairs, vice chairs, secretaries and so on, and the same at county levels, have huge influence on who ultimately gets nominated, and if these party wheelhorses are RINOs, they will work tirelessly to put their own pukey people on the ballot. In fact I’d not be surprised if some of our “MAGA” candidates are in fact, RINO plants, encouraged to run by the RINO party leadership when they realized that Lyn Cheney (and her ilk) were hopelessly compromised as effective candidates. The best way for them to deal with the opposition, of course, is to run it themselves.
Running good candidates is only HALF of the battle!
Biden Gives Us Too Much Credit
…we can move on to the next one.
Apparently Biden (or his puppeteer) has decided we’re to blame for all of the fail in the United States today.
Sorry to disappoint you Joe (or whoever), but you managed to do that all on your own; not only that, you wouldn’t let us NOT give you the chance because you insisted on cheating your way into power.
Yep, you-all are incompetent, and so proud of it you expect our applause for your sincerity. Fuck that!!
It wouldn’t be so bad, but you insist that everyone else have to share in your misery. Nope, can’t have anyone get out from under it. Somehow your grand vision only works if every single other person on earth is forced to go along. So much as ONE PERSON not going along is enough to make it all fail, apparently.
In engineering school we’re taught that a design that has seven to eight billion single points of failure…sucks.
Actually, we weren’t taught that. Because it would never have occurred to the professors to use such a ridiculous example.
Justice Must Be Done.
The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.
Lawyer Appeasement Section
OK now for the fine print.
This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.
We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.
And remember Wheatie’s Rules:
1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.
(Hmm a few extras seem to have crept in.)
Spot Prices
All prices are Kitco Ask, 3PM MT Friday (at that time the markets close for the weekend). (Note: most media quotes are for the bid…the price paid by the market makers, not the ask, which is what they will sell at. I figure the ask is more relevant to people like us who wish we could afford to buy these things. In the case of gold the difference is usually about a dollar, for the PGMs the spread is much wider.)
Last Week:
Gold $2,647.50
Silver $30.62
Platinum $934.00
Palladium $976.00
Rhodium $4,875.00
FRNSI* 127.073-
Gold:Silver 86.463+
This week, markets closed at 3PM Mountain Time Friday for the weekend.
Gold $2,623.40
Silver $29.58
Platinum $935.00
Palladium $948.00
Rhodium $4,850.00
FRNSI* 127.907-
Gold:Silver 88.688+
Silver down over a dollar…which sounds bad until I tell you it went up fifty cents on Friday, and is still down over a dollar. So Thursday, it really sucked. And the gold:silver ratio is getting really, really bad.
The only thing that went up is…miracle of miracles…platinum, which is still on fricking sale.
*The SteveInCO Federal Reserve Note Suckage Index (FRNSI) is a measure of how much the dollar has inflated. It’s the ratio of the current price of gold, to the number of dollars an ounce of fine gold made up when the dollar was defined as 25.8 grains of 0.900 gold. That worked out to an ounce being $20.67+71/387 of a cent. (Note gold wasn’t worth this much back then, thus much gold was $20.67 71/387ths. It’s a subtle distinction. One ounce of gold wasn’t worth $20.67 back then, it was $20.67.) Once this ratio is computed, 1 is subtracted from it so that the number is zero when the dollar is at its proper value, indicating zero suckage.
It Sucks To Be A Flat Earth Charlatan
If you are a flat earth charlatan, my just telling you you suck would be the LEAST bad aspect of your life. How can you look at yourself in the mirror?
As for everyone else (including Flat Earth true believers–i.e., the victims of the charlatans), you all likely know that The Final Experiment (TFE) happened this last week. At this point the participants are on their way home, except for Critical Think, whose flight from Punta Arenas to Santiago Chile isn’t for another day or two. Then he flies directly from Santiago to Sydney Australia…oh, wait, I forgot, that flight doesn’t exist according to Flat Earthers.
In many cases they collected terabytes of data. (“tera” is what comes after “giga” if you don’t know. “Tera” equals “trillion” (twelve zeroes) and that should be easy to remember because both start with t.) One person recorded over 24 hours of 11K video (not a time lapse, full time video) of the sun. Others took numerous sun spot shots (and they have thousands of emails from people like me waiting for them, for comparison). But it’s taking them days to get back, and now they have to deal with the holidays. So don’t expect much out of them before New Year’s. As for the documentary the one flat-earther professional is putting together, who knows how long that will take. They have all kinds of stuff, that should sink this bullshit once and for all, but won’t, because many of their followers are having cult psychology kick in. “Terabytes of evidence against my position? It must be fake. I can’t possibly just be…wrong about this.”
I’ll post a couple of videos here, some of them are repeats. This one is SciManDan, a Glober who was not part of TFE, talking about various types of copium being taken by the Flerfs:
Here’s something new I found. Lots of clips up front of the Flerfer charlatans insisting that what was seen could not possibly exist–which to me would mean that what was seen invalidates the Flat Earth. But these people move the goal posts. Once that evidence comes up, they need something else…yeah, that is what you need to disprove flat earth. (Marred by the fact that Peterson confuses Ushuaia Argentina with Punta Arenas, Chile):
And this is one I posted earlier. McToon (Glober) is letting Nathan Oakley (Flerfer Charlatan) have it with both barrels.
Wolf took exception to this, thinking McToon was over the top. I disagree. Oakley is a fraudster. This is the least of what that species of “human” deserves. They should have “CON MAN” tattooed on their foreheads.
I will, nevertheless post a Nathan Oakley response:
Precession of the Equinoxes
We’ve got a lot of prerequisites fresh in our minds, so let’s take up precession of the equinoxes, a subject that seems to come up frequently. And I’d normally not touch it with a ten foot pole or a lot of graphics. An animation would be best honestly, and I found one but I wish it showed a bit more (like relation with the Earth’s orbit).
Remember this from last week?
Since the Earth’s axis of rotation is tilted about 23.5 degrees with respect to its orbit, the celestial equator is tilted 23.5 degrees with respect to the ecliptic, as shown below.
Last Week
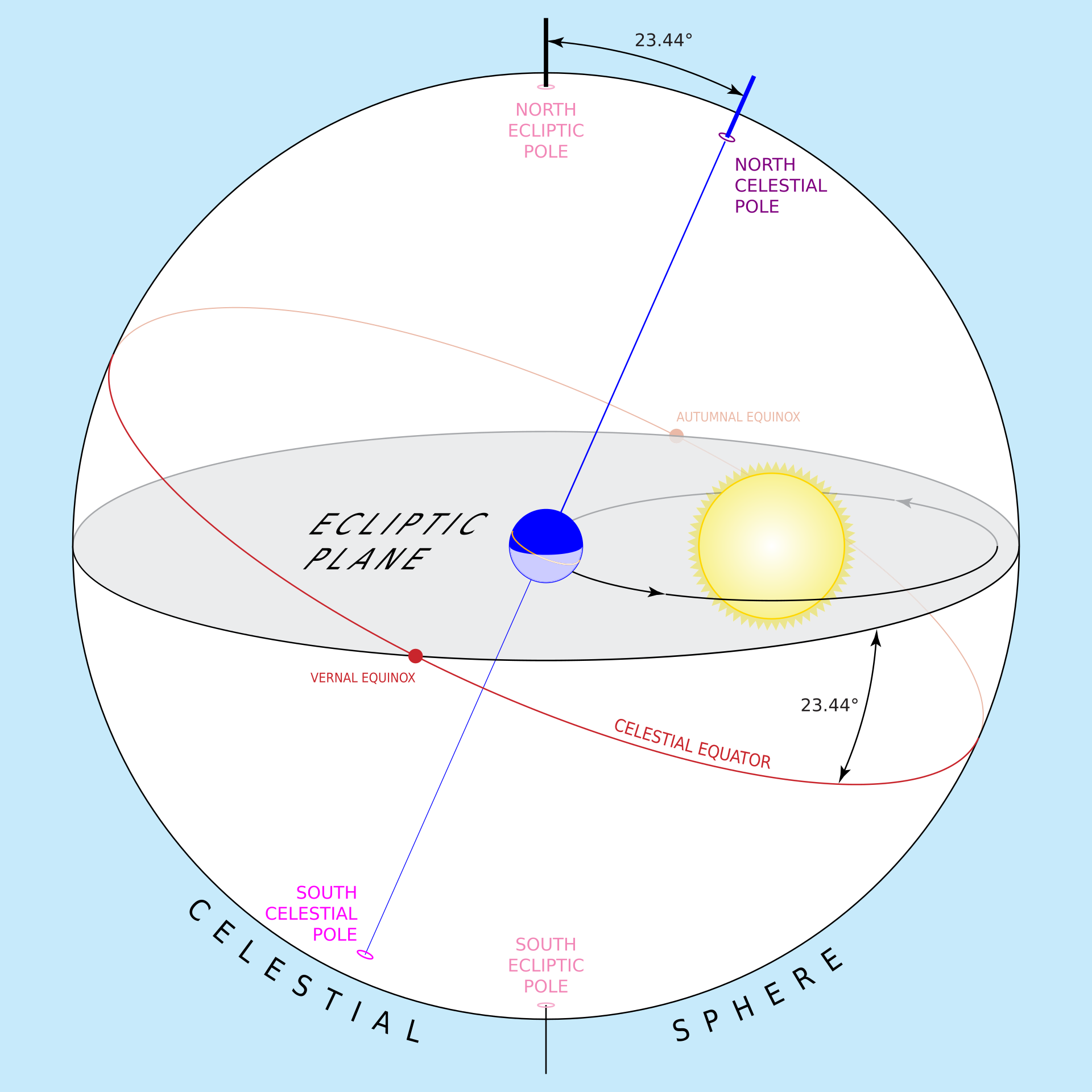
But then I went on to say:
But since we’re thinking in a set of coordinates that goes from the celestial equator, we think of it the other way around: we think of the ecliptic being tilted with respect to the celestial equator.
Me rambling on more, last week
Well this time we are going to think the the way the diagram shows; the ecliptic will be the basis of another coordinate system, known as…drumroll…the ecliptic coordinate system.
There are actually two ecliptic coordinate systems, one centered on the Sun (heliocentric), the other on the Earth (geocentric). Since the planets generally orbit in planes almost aligned with the Earth’s orbital plane (which is the ecliptic plane), and the Sun is the center of gravity of the solar system, the sun-centered system is very useful for talking about the solar system. Indeed, even though I didn’t mention it at all in the recent series on the planets, I have used it here–go back to the articles on the great conjunction almost exactly four years ago; I did those plots in that system.
But we’ll focus on the Earth centered (geocentric) version this time.
For both systems (as well as the equatorial system I talked about) the primary line is the one pointing towards the vernal equinox (or March equinox, or (sometimes) the “first point of Aries”). It lies in the “reference plane” of all systems. For the ecliptic system, the “poles” are simply a line perpendicular to the ecliptic plane; in the diagram above they are called the north and south ecliptic poles.
In the ecliptic system, the two coordinates are called ecliptic longitude and ecliptic latitude and both are measured in degrees; no mucking around with hours of right ascension and minutes and seconds of arc that aren’t the same kind of minutes and seconds as the other minutes and seconds.
In the heliocentric system longitude is represented by l (italic lower case L) while in the geocentric system it’s represented by Greek letter lambda, λ. Latitude is represented by b (heliocentric) or β (geocentric).
Or, if you know the distance to whatever it is you’re considering, you can go Cartesian, a grid instead of spherical coordinates:
x = r cos β cos λ
y = r cos β sin λ
z = r sin β
The x axis points towards the first point of Aries, the y axis is 90 degrees counterclockwise from it in the ecliptic plane, and z points toward the north ecliptic pole. The formula is the same for the heliocentric system (swapping b for β and l for λ) and it was the Cartesian version of the helicentric system I worked with in those old posts from four years ago. (And similar conversions can be done with equatorial coordinates.)
[Digression: Both equatorial and ecliptic coordinates are considered “right handed” coordinate systems. Why? Imagine pointing the fingers of your right hand along the x axis, then bending them to point along the y axis (or, if in spherical coordinates, curling the fingers in increasing longitude or right ascension). Raise your thumb like “thumbs up” and it points along the z axis. On a left handed system, this works for the left hand instead. I find this easier than whiddershins and diesel or whatever those words were.]

Imagine a line drawn from “Autumnal Equinox” through the Earth to “Vernal Equinox.” It’s the intersection of the celestial equatorial plane and the ecliptic plane. (Two planes that aren’t parallel and aren’t the same plane, will intersect in a line.) It just happens to be the case that Earth is tilted in such a way that this particular line represents the intersection (and is the X axis in both the equatorial and ecliptic systems).
What if it were in a different place? It’s pretty arbitrary, isn’t it? Why couldn’t it be in a different place?
It would be, if the Earth’s equator were oriented differently–meaning, also, “if the earth’s axis were pointed differently.” Oh, I suppose the Earth’s orbital plane could shift, but that’s much harder than shifting the poles.
I can say this with confidence because the Earth’s axis does indeed shift direction! It does so without changing the angle between the celestial equator and ecliptic. Over the course of some 26,000 years the line of intersection shifts through a full 360 degrees. (And unlike almost everything else…it goes clockwise.) The first point of Aries precesses and the line points to the two equinoxes, so this is precession of the equinoxes.
If you are having trouble visualizing this, well, we’re both in luck. I found a good animation.
By about 30 seconds in you can see how it works.
The effect of this is to move the first point of Aries (represented with that 
As the first point of Aries moves, the Earth’s axis draws a cone through space, scribing circles on the celestial sphere centered on the ecliptic poles.
There are two other effects of this.
First off, it mucks up both equatorial and ecliptic coordinate systems, because the x axis, the primary axis…is moving! With ecliptic coordinates, you could probably just ignore this…and say we’re going to use the x axis direction from (say) 2000 and just leave it there. Big deal. The fundamental plane doesn’t change. Even if you let the X axis change, the Z axis does not, and you can just add or subtract a correction from ecliptic longitude and be current.
But this precession of the equinoxes absolutely hoses the equatorial coordinate system, because the fundamental plane itself shifts. And we can’t just go on using an old set of axes; the point of the equatorial system is so that you can be assured that if you set a telescope to a certain declination, it will stay at that declination as the earth rotates (even if you don’t have the telescope track whatever you’re looking at). So we issue new charts every fifty years ago, epoch 1950, epoch 2000; with all star coordinates shifted. At some point we will need to switch to something newer–or perhaps they’ll just let computers do the work of listing coordinates according to where the equinoxes are right now.
The other effect is on our year. Just like we have sidereal and solar days, the first being one rotation as seen from the stars, the other being one rotation as seen from the Sun, we have sidereal and tropical years.
A sidereal year is how long it takes for Earth to return to the same spot in its orbit, as seen from far away, in the stars (a sort of “God’s Eye View” of the situation). But our calendar does not track the stars, it tracks the seasons, and the interval between two crossings of the March equinox is called the “tropical year.” We set our calendar up so that the average length of a year (in whole days) is as close to one tropical year as possible. Otherwise, our calendar shifts with respect to the seasons. (We had trouble with that while following the “every four years is a leap year” rule. The calendar would slip against the seasons about 3 days every four hundred years. So we changed the calendar to drop three leap years out of every four centuries. The old schema is called the “Julian calendar” while the new one is the “Gregorian calendar”, each named after the person who instituted the system.)
A calendar year is the interval between one equinox and the next time we’re at that equinox, not (quite) the amount of time it takes for the sun to (apparently) return to the exact same place in the sky.
Actually since a calendar year is a whole number of days, we want the average length of a calendar year to be equal to the amount of time it takes to return to the same equinox (or solstice).
Since, as seen from either the north celestial pole or the north ecliptic pole, the Earth orbits counterclockwise but the equinoxes shift slowly clockwise, the effect is that one tropical year elapses just before the Earth can finish a full orbit with respect to the stars. How much before? About 1,224.5 seconds faster, roughly 20 minutes, 24.5 seconds. You can estimate the exact amount of time it will take the equinoxes to precess by dividing the number of seconds in a sidereal year by 1,224.5 and you get 25,772 years–which invariably gets rounded to 26,000 when you see this talked about in science popularizations. And this makes sense because it happens that the rate itself does vary; it’s not always 1,224.5 seconds per sidereal year.
13,000 years or so from now, Earth will be on the other side of its orbit when springtime hits the Northern hemisphere…but even though the Earth will be on the other side of its orbit, it will still be called March 21, because the calendar tracks the seasons, not the stars.
Speaking Of Earth
Go back through my series of articles on planets, moons, comets, asteroids and the Sun, and it appears I left one thing out, something fairly high up on the list.
The sixth largest body in the solar system.

Yep. I never talked about the third round rock from the Sun, Earth.
I picked that picture because it was taken from the Galileo space probe. The one that went to Jupiter. Before it got to Jupiter, it played gravity assist pinball, getting a boost from Venus then two assists from Earth. It was the first interplanetary probe to return to Earth (though it didn’t linger).
It also took pictures of the Simpson desert in Australia and the Ross ice shelf in Antarctica (the latter is a mosaic assembled from smaller images).


It was useful to see how Galileo’s cameras would behave taking pictures of a known target.
And the Earth is well known; we’ve been stomping around on it for millennia.
So: the basics.
Earth has a radius of 6,371 kilometers. (Try to take so much as one orbital dynamics class without having that number burned into your brain by the time of the final exam.) That is an average. Through the poles, it’s 6356.752 kilometers, through the equator, it’s 6378.137 kilometers. The mean density is 5.513 grams per cubic centimeter…and that is a record for any round body in the solar system. (Metallic asteroids will be higher of course.) It even beats out Mercury which has a large (for its size) core.
Density is useful for helping to figure out what something is made of. A lot of those outer planet moons have very low densities, indicating they’re mostly ice; others have slightly higher densities, indicating they’re more rock than ice…and so on. A typical rock has a density of about 3, and ice is just below 1.
I’ve often talked about the average density of different bodies in the solar system, and you may have wondered how we could possibly know this. It’s not as if we’ve sampled Earth at all depths, much less any of the other bodies we’ve only flown by once.
It turns out we can know this, relatively easily in fact. The average density of some planet or moon is its mass, divided by its volume, so we need to know two other things to get the density. Volume is easy: once you have a radius, r, you can compute the volume of the object via (4/3)πr3. Mass is a little trickier, but we can get most of the way there if something is in orbit around the body. The orbital speed for a circular orbit is v = √(μ/R). Since we’re after the mass, let’s rearrange that a bit: v2R = μ This time R stands for the orbital radius (not the radius of the planet). That other letter, Greek mu (μ), is the gravitational parameter of the body–that’s different for every body. So if we know the distance between the satellite and its primary, and we time how long it takes to orbit (T), we can get the velocity readily (2πR/T). We can substitute into the first formula and get μ = 4π2R3/T2 And then we have this “gravitational parameter” thingie, based totally on the orbital radius and the time it takes the satellite to orbit.
(Gravitational parameter is another thing we had burned into our brains…but at least I’ve managed to forget its value since then. I just looked it up, Earth’s gravitational parameter is 3.986 x 1014 m3/s2. Except I was used to deal with kilometers per second, so I used 3.986 x 105.
But we wanted mass. Well it turns out that μ is equal to the mass of the primary, M, times the gravitational constant, G. But that’s as far as we could go for about a hundred years; we could measure μ, but we actually had no idea what G was, so we couldn’t get from μ to M. In the late 1790s Henry Cavendish was able to measure the gravitational force between known masses, so this time, he knew the mass, and could compute G. As soon as he did that, every known value of μ, be it for Earth, the Sun, Jupiter, Saturn, could be used to compute a mass. So.
Earth is being orbited by the Moon, so we could do the calculations above and arrive at the total mass of the Earth, then divide by the volume. If a body didn’t have a satellite, though, we were SOL. So we found ourselves in the situation where we knew Uranus’s mass better than we knew the mass of Venus, even though Venus is much closer. Uranus has moons, Venus does not. And of course moons themselves didn’t have anything orbiting around them, so we couldn’t determine their masses, except in the case of our Moon, which is big enough to have a noticeable effect on the Earth.
Once we could send spacecraft out there, though, we could determine masses, by watching how much their trajectories bent as they flew by. That’s a hyperbolic orbit, and the formulae for it also contain μ.
So with Earth being far denser than typical rocks, what’s inside of it? One cause of higher density might just be that rocks deep down might compress some under the weight of the rocks above them, and we now know that this is part of it. But we still need Earth to be largely made of stuff quite a bit denser than average ol’ rocks.
And so we get something like this diagram (which is not to scale, the ocean and crust are drawn much too thick):
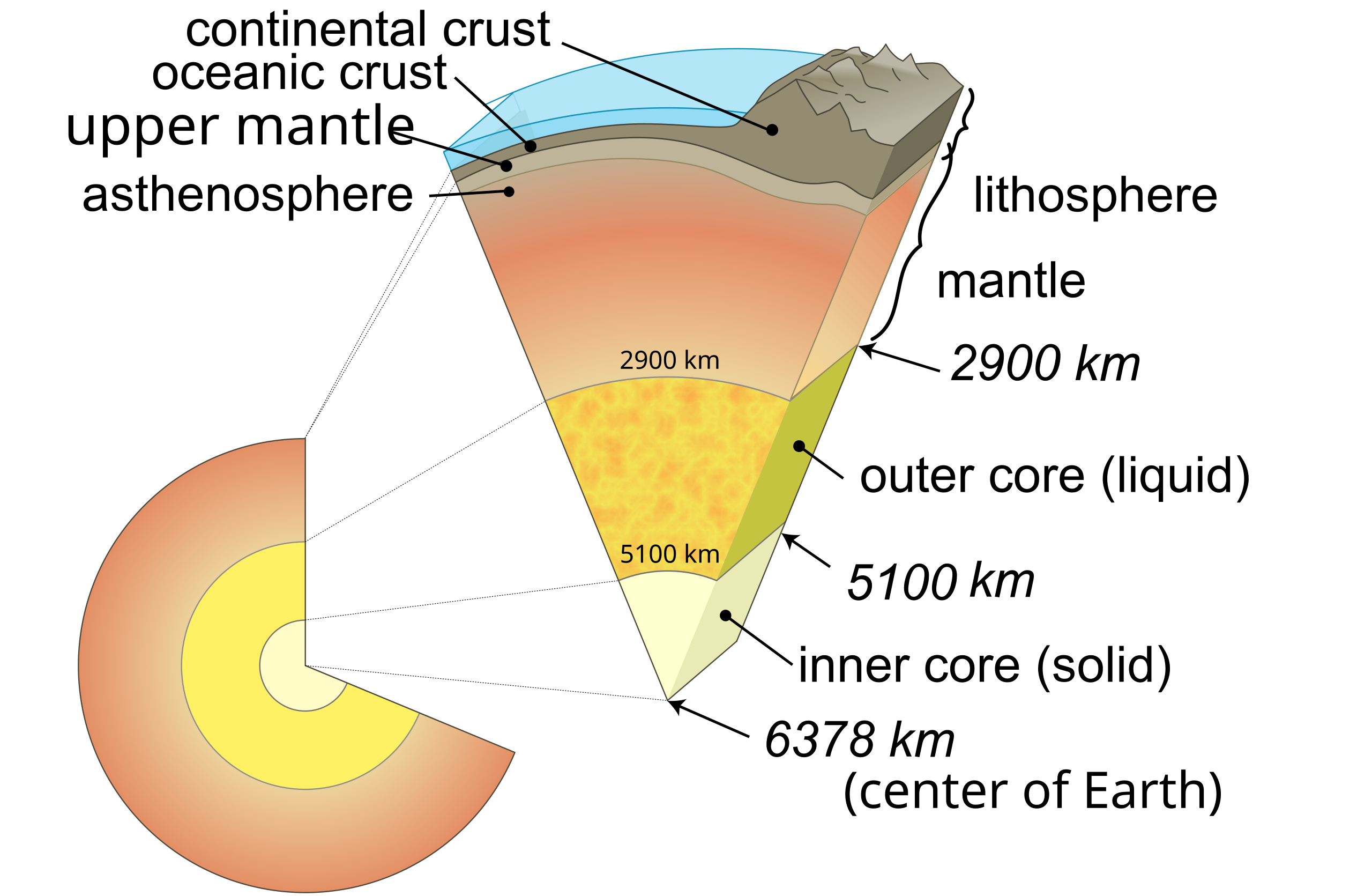
The liquid outer core and solid inner core are believed to be composed mostly of iron, with densities ranging from 9.9 to 13.1 grams/cubic centimeter. (Iron on the surface has a density of 7.874–clearly the iron in the core is compressed.) But given that we can’t drill down even to the mantle, much less down to the core, how do we know this? We can kind of guess that the innards are iron, since iron is very common in the universe (supernovas happen when stars try to fuse iron; the supernovas end up basically barfing the iron out into space). And we get meteorites consisting of mostly iron, to reinforce that. But liquid? How much?
That one’s a bit harder than computing average density. But the answer, in one word, is “seismology.”
If you think I’m just going to leave it there…you don’t know me very welly.
Seismic waves are waves through the solid material of Earth, resulting from earthquakes, volcanoes, movements of magma underground, and even man-made explosions. There are all sorts of different kinds of seismic waves, and different ways to divvy them up.
One is surface waves vs. Body waves. Surface waves travel along the surface of Earth, while body waves travel through the whole body of earth. Surface waves will tend to get weaker in proportion to distance, while body waves will get weaker in proportion to distance squared. (There’s a good intuitive reason for this. Think about a surface wave traveling away from its source ten kilometers. The entire energy of the wave is contained along a circle 2π x 10 km in circumference. Wait for the wave to reach a 20 km distance, all of the energy is distributed along 2π x 20 km of line. Twice as much, so the wave will be half as strong. Body waves travel outwards along consistent hemispheres, not circles, and the hemisphere’s area multiplies by four when the radius doubles.)
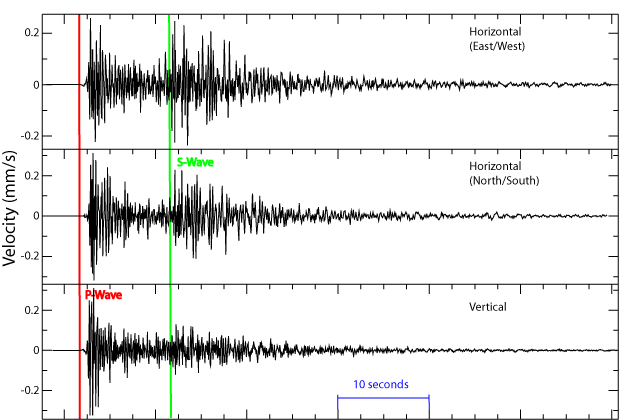
Body waves, in turn, come in two types: P (or primary) waves, and S (or secondary) waves. These names come from the fact that the P waves move faster, so they reach seismographs first. Below is an example, the P wave hits, then the S wave.
The two types are fundamentally different. P waves are longitudinal…which means that the medium the wave is traveling through moves in the same direction the wave is moving. This is very much the way sound works; the sound wave consists of denser and less dense atmosphere and the air molecules move towards and away from the sound source to build up bands of compression and rarefaction. Below is a diagram of a longitudinal wave traveling from left to right.

I said they are much like sound waves, and in fact when a P wave reaches the surface, it will often make a noise. Travel speeds are 330 m/s in air, 1450 m/s in water and 5000 m/s in granite.
Secondary waves are transverse (like light waves).
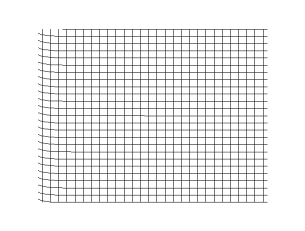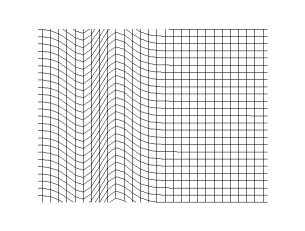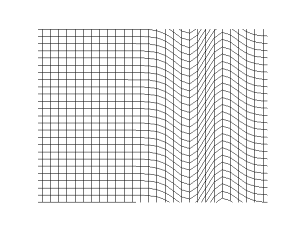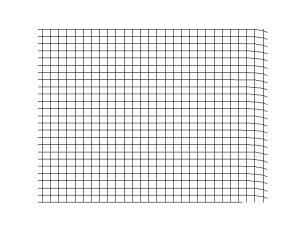
They take roughly 1.7 times as long to cover the same distance as a P wave, and there is one other key difference: They don’t go through fluids. P waves do but they will bend. In fact both will curve when the density of the medium changes (this is another example of refraction).
So we can glean some information about what’s inside the Earth just by looking at how seismometers in different parts of the world react to strong earthquakes. S waves never show up more than 103 degrees away from the epicenter of an earthquake, beyond that, you are in the S wave “shadow”–a shadow cast by a liquid layer deep inside the Earth. P waves have a much complex shadow pattern, as seen below, caused by an abrupt bend in the wave at the core boundary. The core doesn’t stop P waves, but it does bend them sharply.
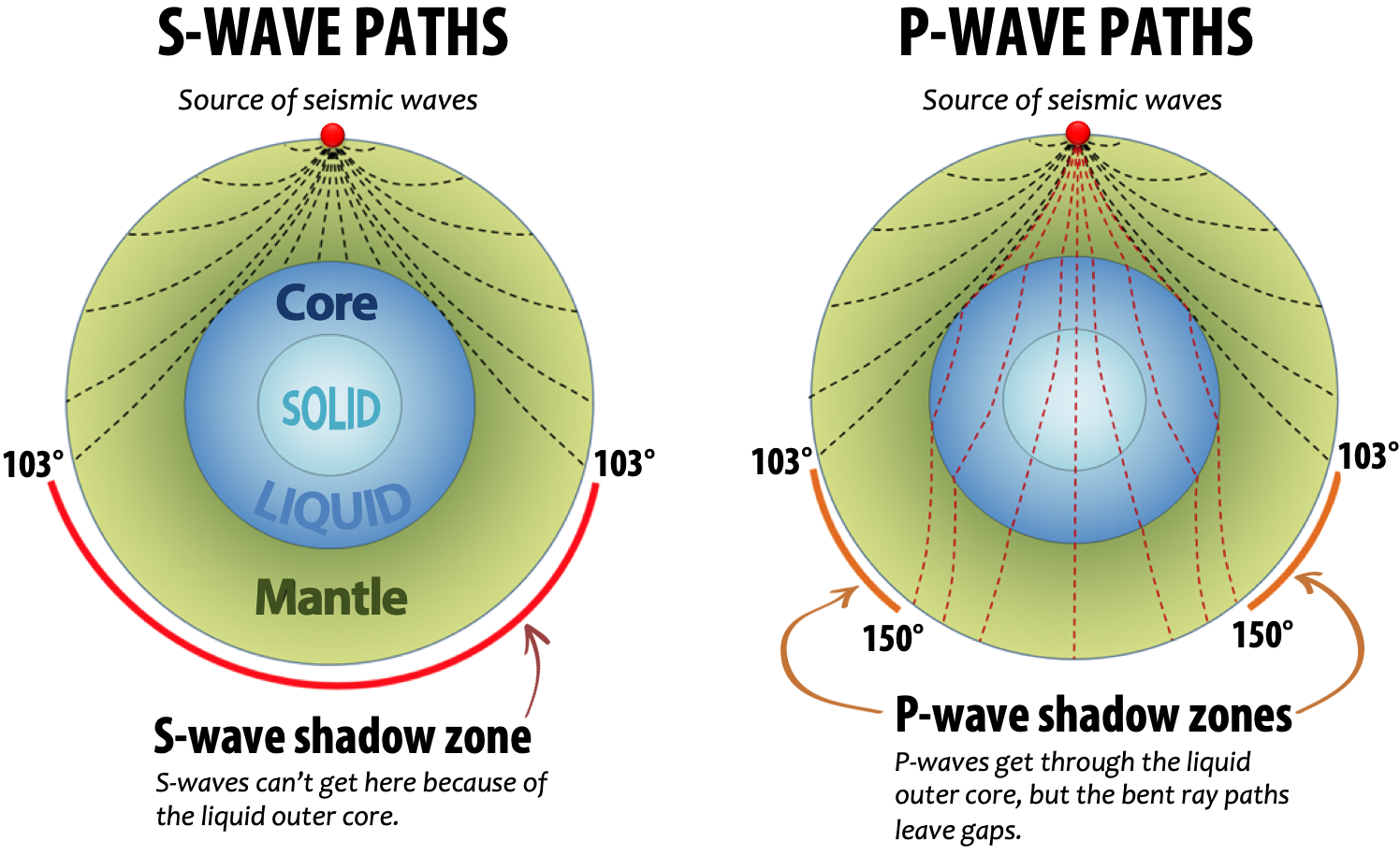
So we know we have a liquid core outer core. How do we know what it’s made of? It does cause Earth’s magnetic field so we know it’s a metal. Meteorites (which came off other bodies of the solar system) come in many different types but occasionally one will show up that is almost pure metal, and that will be roughly 90 percent iron, ten percent nickel. (In fact the meteor that created the Barringer or “Meteor” crater in Arizona was an iron-nickel type.)
So that’s the beginning of how we know what’s inside there. We get the occasional mantle rock brought up by geologic processes, too.
[It just occurred to me this is another bit of evidence for a globe shaped earth. S wave shadows exist. Plot them on a globe, and compare to the origin of the waves. Then do the same on the flat earth disc. Which of the two patterns is symmetric and simple to explain, and which is just some random-seeming curve-bounded area with no obvious physical explanation? I don’t think I’ve ever seen anyone else bring this up.]
I’m going to leave it there.
“But Steve, you skipped over Earth in your series on the planets, and this is all we get?”
You proceed from a false premise. This isn’t part of the series on the planets and moons and other stuff in our Solar System. That series is over.
This is the first part of a new series, on geology. There will be more, lots more.







Hello.
I wish my feral tom was that polite. I can not go out side anymore without tripping over him!
A feral cat that I have tamed acts similarly. I surmise that they want to feel in control, but I’m not a cat psychologist, LOL.
He does figure 8s around my legs. It makes it very hard to walk.
Threats will avail you not!
Flerfers see a photo like this and think the moon is round but the Earth is flat…
Or maybe they claim it is faked.
Anything taken from space is faked, in their minds. Absolutely anything.
Yup. If they can’t get up there to verify, then it’s declared fake.
Great question – will we live to see “SHILL!” being yelled at some flerfer who takes a ride in an Elon Musk vehicle? While all the others refuse to go on the “Final Final Experiment”?
So predictable. And THAT is science! 
Now: Anything coming from Antarctica is fake. Meanwhile, Antarctica proves flat earth! Logic! 

As far as I can tell, that’s two distinct groups of Flerfs. Some say the recent events in Antarctica are faked, the others are either, “this doesn’t matter” (Often expressed as lights in the sky have nothing to do with the shape of what’s under our feet.) or they are now claiming it’s predicted.
There seems to be a new model they’re pointing to but my attempts to learn what it might be by my refusal to listen to stream-of-consciousness rambling.
I have a bad explanation I could loan them, but I refuse to do so. It would just shift the “final final experiment” to a new place for Oakley to lie about.
This one seems to be about the sun they saw being a reflection in the Dome.
That dome, by the way, is why space as we think of it simply doesn’t exist in their view. To say nothing of the fact that Newtonian gravity also can’t exist in their view.
lf they’re going to move the goalposts every time facts are presented, they’re not worth engaging with, IMO.
Yes. Flat earth is psychologically diseased science, which cannot progress past direct sensory experience and immediate complete understanding by all participants in unison.
aka fake science cult
I recently learned about some research that posits that people fall into one of four personality “tendencies:”
https://gretchenrubin.com/four-tendencies/
The absolute dumbest one of these is, to me, the rebel. Where I come from, this is called cutting off your nose to spite your face. This is how I think of people who are flat-earthers. Nothing anyone shows them will make them change their minds, and nothing they see for themselves will either. They simply “rebel” against everything as a knee-jerk response. I call them contrarians. They are simply against everything, no matter how damaging that is.
Not disagreeing.
I notice the four tendencies seem to all be in terms of “how these people will respond to others expecting them to do something.” Maybe I’m reading “do” (n the sense of taking an action, working towards a goal) into that.
Another thing about FE (and many other “oddball” beliefs) is that the holders take pride in seeing the “real truth” where everyone else is brainwashed or oblivious or indoctrinated. That puts them “above” us in their minds…when in reality the opposite is true at least with regards to their ability to evaluate the world.
This is what Ayn Rand called “counterfeit individualism.” A real individualist looks at whatever it is and decides, based on their own criteria, whether they approve or not. Doing a blanket “I disapprove because others approve” is simply a different way of letting other people decide what you think and how you will evaluate things.
Yes, it is. Drives me nuts. But they “rebel” even against their own interests, which is very weird to me. Even when they know it is better for them, they don’t want to do it.
It will make sense in the fullness in the Age of Aquarius!
/s if needed.
LOL!!!
What about people with psychic remote viewing capability?
LOL!!!
Son of Lurch!
Here is the show more along with a few more items.
Ian Miles Cheong
BREAKING: According to reports from UAE and Saudi Arabian 𝕏 users, the perpetrator of the Christmas market attack in Magdeburg, Germany is a fugitive from Saudi Arabia.
The German government refused to extradite him despite requests from the Saudi government, citing human rights concerns.
Translation by @AD_GQ
: “Reports suggest that the perpetrator of the Germany attack is a well-known fugitive traitor named Talib Al-Abdulmohsen. He fled from Saudi Arabia, where he is a wanted individual, and was granted asylum and citizenship by Germany, which refused to extradite him to Riyadh under the pretext of human rights and freedom of expression. He repaid this favor today by committing a massacre.
Europe is destroying itself from within.
End.”
________________________________________________________________
Another Quote tweet from
Elon Musk
·
18m
Absolutely Quote
@HSajwanization
·
6h
It is insane to even process that Saudi Arabia previously requested multiple times to extradite the perpetrator of Germany car attack, and German authorities and Europe ignored them !
________________________________________________________________
Another Repost Tweet from
Elon Musk reposted
@Moraqeb2020
____________________________________________________________________
One tweeter sent the following https://twitter.com/Moraqeb2020/status/1870271155845902483
I can only guess that Musk is now wanted by Interpol for violating Germany’s Speech Laws.
If you missed the doctor plowing through the crowd story it is here.
SHOCK VIDEO: At Least One Dead, Several Injured After Driver Plows Through Christmas Market in Germany in Terror Attack – Update: Suspect From Saudi Arabia Cristina Laila Dec. 20, 2024 2:00 pm 857 Comments
https://twitter.com/Breaking911/status/1870187306247958874
The Most Important

Those are called Merkel Legos…..
Or these:
He was aligned with Al Waleed. Same ilk as Soetoro, Clintons, Soros, etc. Same camp of murderers.
The euro leaders sold out their countries to this intentionally.
Lesson – they did the same to us here in America, which is why PDT and Homan are so intent on taking out the trash.
Folks need to consider reading Joe Lange’s series if they have not. Well written and sourced. You can then see all of the pieces on the chess board and know the team they play for and their roles.
Those who ignored the warnings should be prosecuted.
The Left: “We must show tolerance and love.”
Trump: “You knew I was a snake before you took me in.”
And now people have died and are injured because they took in the snake.
Rampant disease in Europe.
Dumbassery.
Merkel has basically stuffed the ENTIRE political arena (except for the AfD) with sycophants who only obey the globalists and WEFfenSS (but I repeat myself)…
No bench, no backups, only puppets. Again, the AfD are the only TRUE opposition, and the only true hope… and the people here are being brainwashed by the YSM/MCM and the entire leftard “ed biz”…..
“Those who ignored the warnings should be prosecuted.”
____________
Waaaay past that.
CTH says 200+ people were injured, and multiple fatalities including at least one child.
Every government building in Germany should be on fire right now, with the People waiting outside to deliver justice to those who decide to risk exiting the buildings.
Various agencies going back to 2008 were warned about him, but have done nothing. The police in Magdeburg still are looking for a motive…












Islam has disowned the guy as we see with the posts below, but discovered something else. “He is a Zionist” has been trending along with a couple other tags and it’s loaded with the guys screen shots.
Seems the guy is ex muslim. He did the walk away and became a pro Israeli Zionist atheist and LGBTQ lover.
Because these were all screen shots I wanted to see if his tweet page was still up but was met with this.
Well that was wrong. It may have came down, but it’s still up as I post here.
https://x.com/DrTalebJawad
From what I could see he was definitely an atheist, pro LGBTQ and had walked away from Islam a long time ago. Was angry at the Euros for allowing it to fall to Islam. Seemed supportive of Israel etc…
I didn’t see any anti Christian stuff but it might be in there as well. Others are claiming that as well.
Best I can tell is Stew Peters, whom I’m no fan of has it right when he says this.
https://twitter.com/realstewpeters/status/1870462674066383270
https://x.com/goddeketal/status/1870255335283261715
__________________________________________________________
Meanwhile there is this!!!
https://twitter.com/elonmusk/status/1870482941496947150
Elon Musk
@elonmusk
The atheist angle was a scam to avoid extradition
Quote
Ian Miles Cheong
@stillgray
·
7h
Read this thread. The Magdeburg attacker was a fugitive from Saudi Arabia who was wanted for rape, who reinvented himself as an atheist activist in order to secure full asylum from Germany. x.com/salansar1/stat…
Ultimately this is one seriously twisted snake.

It’s all Taqiyyah….
He’s a flaming Islamist, and it’s all over the alt media.
The YSM/MCM and Israel-hating media be damned. Even Saudi warned about him.
I came across this post:
Makis FenBen and Ivermectin Dosages for Anticancer Treatment – Literally the most effective Onco treatment I’ve witnessed in decades — from peer-reviewed study
I don’t know whether this has been presented here.
I don’t have a link to the article. Someone in the comments mentioned this, too:
https://pmc.ncbi.nlm.nih.gov/articles/PMC9720275/
“The magic bullet: Niclosamide”
Great stuff! Thank you!!!
YW!
Via Yandex.
https://www.sgtreport.com/2024/11/new-treatment-for-cancer-targeting-cell-respiration-and-mitochondrial-function-has-been-published/
https://pubmed.ncbi.nlm.nih.gov/38668357/
https://www.semanticscholar.org/paper/Targeting-the-Mitochondrial-Stem-Cell-Connection-in-Baghli-Makis/dc31f27f53ea0443e9a1dd7af942bdac8f3aea01
https://isom.ca/article/targeting-the-mitochondrial-stem-cell-connection-in-cancer-treatment-a-hybrid-orthomolecular-protocol/
Also transferred.
Thanks for those links.
Transferred that to:
STOP PRESS: New Study Confirms the Shedding of the COVID-19 BTI (Bioweapon Toxin Injections, aka the COVID-19 “Vaccines”)
So it does not get lost.
Also transferred to:
My Cancer Journey (by Linda) and 20241204 Open Thread
I was admonished last night for assuming what I have going on is a result of vaccine shedding. Well…at this point does it matter? What is fatigued is my abdominal muscles, and that is part of the healing process as I understand. Everything I’ve read says just don’t overdo it.
How much Vitamin C again?
I go for 1,000mg It is water soluble so overdosing just gives you the runs (BTDT) I have to take 500mg morning and 500 mg evening which is better anyway. Again because it is water soluble so you body gets rid of it fast.
It is the oil soluble vitamins like A that can be dangerous.
I was encouraged to take this:
That is what I take if I get sick. I am staring at a Raspberry flavored version.
When I am sick, the 1,000 mg does not bother me. Go figure!
Okay, I used twice the water recommended and got 3/4 of it down. Starting slowly.
I would like to do 500 morning and evening, but not with that product.
500 mg tablets of C are quite common and available at all the big drug chains. They all seem good to me!
Buffered vs. non-Buffered made a big difference for me.
I like hot peppers, Red Hot sauce, etc., and almost nothing bothers my stomach. But regular (non-buffered) vitamin C capsules did not agree with my stomach.
The buffered kind were fine, didn’t bother me at all.
I take a 750mg capsule of Vitamin C every day with dinner. I tried regular vitamin C first, and my stomach didn’t like it.
Switched to BUFFERED Vitamin C (750mg) and no problem.
I have had NOW brand before, currently taking California Gold Nutrition ‘Buffered Gold C’ brand, either one should be available at Amazon or iHerb
I do 1000 mg, Trader Joe’s brand, nightly after dinner. 1111% of US RDA.
“I go for 1,000mg It is water soluble so overdosing just gives you the runs (BTDT)”
____________
Well that doesn’t sound very pleasant.
I’m not gonna to try to figure out what the acronym stands for…
“Been There Done That”.
DePat
I take 2,000mg of Vitamin C daily. I had to “build up” to this amount over a period of time. IMO, it’s also important to make sure one is hydrated.
Trying to hydrate. If I get the water too cold, it’s asking for trouble. Just spent ten minutes coughing up watery stuff.
Like I said, my immune system seems to be fine. It’s the core muscles that are working even more overtime than usual that are the issue. One spot that had been bugging me walking for at least six months prior to this in particular. Sometimes, it feels like I just got started on Pilates again.
You might find nicotine gum very helpful as nicotine has a strong affinity for the ACE2 receptor and will push the Spike Protein off of it.
It was talked about yesterday in a video with Mike Adams and Dr Lee Merritt.
https://www.brighteon.com/c3134c9b-16e3-41bd-8053-774a8f3b935e
THis is the second recommendation for nicotine. The other was using a quarter of a patch. I really should not chew gum other than when descending from cruise altitude in a plane due to tightness in the jaw. All singers have to deal with this.
They claim it has fast results, from instant, to overnight, to feel better than ever…
“THis is the second recommendation for nicotine. The other was using a quarter of a patch. I really should not chew gum other than when descending from cruise altitude in a plane due to tightness in the jaw. All singers have to deal with this.”
____________
Marlboro reds or Lucky Strikes should do the trick then
Not with singing.
Maybe a pinch of Copenhagen….
Singers used to be a heartier lot.
I saw Jim Morrison in a live performance (on yootoob) light up and smoke a cigarette during the long instrumental part in Light My Fire just the other day
No. No smoking.
“Everything I’ve read says just don’t overdo it.”
____________
Good instructions for cooking steak, too

Thanks, TT! Saved on my computer.
YW!
TheseTruths
Thank you for this.
Here is the PDF of the article which has this information from the Journal of Orthomolecular Medicine, Vol. 39 Number 3, 2024:
https://isom.ca/wp-content/uploads/2024/09/Targeting-the-Mitochondrial-Stem-Cell-Connection-in-Cancer-Treatment-JOM-39.3.pdf
The International Society of Orthomolecular Medicine is based in Canada.
Dr. William Makis and Dr. Thomas Levy are heavily involved, as well as contributing articles to the society’s Journal.
IMO, this article is further confirmation that the ingredients and mechanisms of the COVID-19 BTI (the “vaccines”) target and damage the MITOCHONDRIAL CELL LAYERS AND MECHANISMS of the “vaccinated” person’s body. This is crucial to understand how these injections damage / destroy organs and mechanisms of the “vaccinated” person’s body, inducing literally thousands of negative health reactions and conditions among “vaccinated” persons — among these, cancer.
Good info; thanks!
Two years ago May, I was diagnosed with what was assumed to be stage IV rectal Cancer. I didn’t do any scans to see the extent of any metastasis. I didn’t need or want to know as it would not have changed the treatment plan.
Right away I bought my own ozone setup for insufflations.
I started getting high dose Vitamin C IV, as high as 100grams a session, which was done at home. Both are considered adjunctive therapies, although plenty of information shows they are very effective on cancer.
After 12 months, the cancer marker, CEA had improved to a stalemate, and I was on the losing of the stalemate. 34 to 13, normal is < 2
So Ivermectin was added in July, and from links from Qtree, it helped to establish my confidence in trying Fenben, as it made sense; starve the cancer.
So I have been following the protocol from Orthomolecular to get the dosage right for Ivermectin and Fenben. It takes time to work your way up to the recommended dosages.
There was no improvement in markers in August, but major improvement in December, to 5.7.
There is a moment when you know the tide has turned and you have returned to the living.
I hope this was helpful.
Magnesium Reversing Disease by Dr Thomas Levy was also extremely helpful.
Zopa, such wonderful positive news! Thank you for sharing.
When you are of a mind to, updates always welcome.
2025 is gona be a great year!!!
Inspiring – thank you for sharing!
How Vitamin C and Magnesium Help Reverse Disease — Lewrockwell.com›2020/04/joseph-mercola
2 hour Youtube:
zopa
What good news! Kudos to you for determination and grit!
TY for sharing this. God Bless YOU in your continued healing process. This would be a great comment to copy to Linda’s healing from cancer post from the other day
that would be good..
I did move it to that article.
TY
That is amazing great news, Zopa!
Very helpful. I save all posts like these. There is real hope for cure now with these treatments, and the more positive results and personal experiences there are, the more confidence it gives others to try these kinds of treatments.
Thank you for posting about it, and I hope you are on the way to a full recovery!
I’ve been alternating days between sponsored and unsponsored OKGO videos. In this one, Chevy gave them a car!
It also involves a large number of pianos and guitars, and a multi-day stunt driver training course for Damien Kulash, the lead singer. At one point, he’s driving at speed along a 70+ foot drop-off, so I’m sure the previous coursework was appreciated by all concerned.
….and, then, there’s this one. It might not count as “sponsored”, because they did set pieces with other guests on this show, but…..
In Steve’s cross-section of Earth illustration, the outer solid layer of the Earth is labeled “lithosphere”. This incorporates the Greek word “lithos”, which means “stone”. Thus, the lithosphere is the sphere of stone.
This root is also found in “paleolithic” — relating to the old stone age — and “neolithic”, which relates to the new stone age. Lithography involves inscribing a picture in stone (nowadays linoleum is preferred), filling the scratches with ink, and pressing the picture onto paper.
And “lithium” although there is very little lithium in the lithosphere.
As well as “monolith” (one stone); “regolith” (“blanket stone”, loose crud over stone); and “megalith” (major stones, like stonehenge, which was aligned with the winter solstice just a few hours ago).
Had no idea….
NEW: Crowd goes absolutely nuts after professional darts player Christian Kist hit the first nine-darter of the World Darts Championships.
I never knew darts could be so electric.
The nine-darter by Kist meant that £60,000 was donated to Prostate Cancer, £60,000 was given to a fan in the audience and £60,000 was pocketed by Kist.
https://twitter.com/i/status/1869789370133180831
the only darts i ever played was lawn darts–those projectiles you threw in the air and hoped would land in a ring and not in the neighbor’s dog…
One of the bars here used to have an annual international tournament. I know/knew people who were in leagues. Darts can be a lot of fun.
is there a cordoned off area in the bar? cuz drinking and throwing sharp objects seems antithetical to me…lol
THere’s a whole room on one side with an elevated barrier for drinks, and, back in the day, ashtrays. It’s actually quite functional.
LOL, we were in one of those places yesterday, except the ash trays were outside.
Nowadays they are, but back in the 90s there were places you couldn’t see across the room.
I always hated cigarette flavored meals, where my eyes were streaming and I was constantly sneezing.
However I stood up for allowing employees the right to smoke in their car during breaks. The company I worked for BANNED smoking on the property so the factory workers had to walk a 1/4 mile to get a smoke…
RESULT?
Some one snuck a smoke in the warehouse resulting in an explosion that blew a big hole in a concrete wall.
I was in those too
Jarts! We’ve got the old metal tipped ones at my parents’ Cottage
those are the ones!
My dad & grandpa played regularly w/ a half dozen school age kids running around & no one got hurt, that I can recall
Reminds me of playing darts in college at the bars.
It’s hard to throw a dark normally, trying to arc it to the dart board. And I couldn’t figure out what the fins on the dart were for, because it wasn’t going fast enough for the fins to do anything.
So I came up with a new way to throw darts.
You hold the dart in the palm of your throwing hand, with your hand open, you don’t hold the dart with your fingers at all. The fins are next to your thumb, and the point of the dart is sticking out past your little finger.
Then you wind up, just like you’re throwing a fastball, and throw it hard. Not as hard as you possibly can, I tried that, and it’s fun, but you lose a little bit of control. If you back off about 15-20% from throwing as hard as you can, you maintain plenty of control.
The dart, held loosely in your palm, rolls across the palm of your hand and off your fingertips as your arm goes forward in a baseball throwing motion, giving the dart a lot of spin as it leaves your hand.
And it’s not doing some dopey little arc either, it’s a straight-line laser shot. Buries the tip of the dart about 3/4 of an inch into whatever it hits, so you want to practice with old beat up darts and a board hanging on a wall that can take some abuse.
After an hour or so, you get the hang of it pretty well. It worked better for me than trying to ‘push’ the dart through the air the normal way, and it was a lot more fun.
Gets everybody’s attention at the bar too, when those darts hit the board at around 70mph…
THWACK!
Nostradamus was born December 14 or 21 in 1503 (couldn’t get a definitive date) and this prediction made me go…hmmmmm too.
Thankfully, not real Nostradamus!
(I hate quoting Snopes, but they went looking for it, and say they couldn’t find it.)
https://www.snopes.com/fact-check/nostradamus-predict-feeble-man/
Even if it were, it’s annoyingly vague.
It doesn’t pay a prophet to be specific.
precisely!
That would ruin their prophet margin…
good to know…i did an open about him today–concentrating more on the man than the predictions. most are too wide and open to interpretation.
Often you will find when a quote is put into a non searchable block of texts like the image above, it is false. Not always but often.
If it was searchable you could drop it into a google search engine and it should pop up. Example Cuth drops a poem in a post and I’m confused if he wrote it or someone else did. I just copy the poem and search the full thing to find out it’s origins.
This one is indeed false as this points out.
https://www.google.com/search?q=A+plague+shall+fall+upon+the+world.++After%2C+a+feeble+man+shall+rule+the+western+World+with+a+jezebel.++The+people+will+be+damaged+and+subjugated+by+a+fool+ruler.++The+great+eagle+shall+suffer+and+fall.++Nostradamus&sourceid=chrome&ie=UTF-8
A few other things. This does not mean it was not once a prophecy and the prophecy could have had Roman origins as it mentions the great eagle, a symbol of Rome and it mentions a fool king and a jezebel wife. This leads me to believe that it was meant for Eastern Roman Emperor Justinian and his whore wife (though it could be for another but Justinian was rather controversial in his time, Bill and Hillary Clinton level). If that is so, one should note that Nostradamus was alive December 1503 – July 1566 which immediately disqualifies the quote as coming from him.
Which Justinian?
The famous one reigned in the 500s, had to deal with the Nika Riots where 30,000 died (over chariot racing–and you thought British soccer was bad). build the Hagia Sophia…and then actually reconquered almost half of the (now fallen) Western Roman Empire. He couldn’t get Gaul, Iberia or Britannia back.
Yes. The one there during the Nika Riots! Crazier times than ours!
Also first to solicit money and raise taxes for Climate Change claiming the Aegean Sea was on the rise and important buildings needed to be protected.
General Prokopios who wrote “The Wars of Justinian” while the Emperor was still alive, had all the inside scoop and dished it out after Justinian died in his “The Secret Histories” which might qualify as one of the first great tell-alls except it was covered up and not rediscovered until some Vatican Monk in the Middle Ages was likely ordered to scoop up some stuff from the archives to prove some obscure point that supported the Church.
British Krikkit is worse…
(including death by boredom)…
truthorfiction.com used to be a decent alternative to snopes…
It “fits” too many current events by packing COVID, Biden & Commala, and America all in one handy paragraph. Nothing Nostradamus said was ever so specific where you could definitely say he meant “whatever” event of today.
Nothing Nostradamus said was ever so specific where you could definitely say he meant “whatever” event of today.
Yup. That’s our Liz!
I hate hearing her called “our”s, but I suppose it’s true. Our deuce waiting to be flushed. Our cancerous tumor.
Love it! And TRUE!!!
Charlotte99
December 21, 2024 4:46 am
Senile Biden’s insult to families of Marines murdered in disastrous Afghan withdrawal
Joe Biden kept the grieving relatives of the Marines killed in Afghanistan waiting for three hours while he napped on Air Force One on the tarmac before a dignified transfer, multiple military families have told Daily Mail.
The shocking allegation comes today amid growing calls for the Biden administration to be investigated over its scandalous cover-up of the president’s ailing health.
Biden, it has emerged, has not been present for key moments of his presidency, nor has he been involved in major decisions like the disastrous withdrawal of US troops from Afghanistan in August 2021.
https://www.dailymail.co.uk/news/article-14210847/biden-insult-senile-health-coverup-marine-families-afghanistan.html
The investigation should be on Maggots administration, politicians and Pravda News who knew Maggot was incompetent. They denied it. Covered it up.
it draws into question the legitimacy of EVERY EO, EVERY PARDON, EVERY DECISION “he” ever made.
Agree. Common sense.
That said, PG insists what is done, is done.
The fact Maggot was installed, aside for a moment.
LeadershipAssholes in power Allowed The Maggot Travesty for four years.I’ve been bitching about this for several years. Minority opinion, I spose.
i dunno. if an elderly person is coerced into signing over their home or life savings…isn’t there a remedy for that?
how is this any different?
This indicates there are STATE LAWS.
FINANCIAL EXPLOITATION OF THE ELDERLY THROUGH UNDUE INFLUENCE: HOW TO SPOT IT AND WHAT TO DO ABOUT IT
From Brave AI
>>>>>>>>>>>>>>>>>>>>>>>>>>
This possibility may be why the installation of the Hoe before Jan 20th may be attractive.
OMG – I just realized. Biden may not have pardoned all the right people for Obama and Hoe. They may want to take him out, for a new set of pardons that help people Biden refused to help.
Bribed judges make it difficult to pursue legal remedy. You need a good lawyer for that. That said I think we go into over drive there when speaking of the Biden’s.
It all proves the Uniparty being in control as was played out in Congress just this week. It also proves there are multiple illegal legal systems that administer justice based on standing and/or alignment.
You read my BIMD – readers were given some of my first hand experiences. They confirm your statements. I believe there are more than we realize who share our opinion. They just shrug their shoulders and go on about their day hoping somebody else will handle it.
Interesting that the plot of Gladiator II comes in strongly on the question of corrupt and despised leaders, “insurrection”, and the legitimacy of empire over republic. One might even say that “Fake News” makes an appearance! 
Gladiator II?
Holy crap.
The First gladiator movie begins in 180 CE…the end of the reign of Marcus Aurelius.
From that day forward, the Roman Empire was sliding down the shitter, IRL. Constant civil wars at least until the reign of Diocletian (who removed all remaining pretense that Rome was a republic–historians call the empire up to that time the principate, because the emperor was the “first citizen”; after that it’s the “dominate”). Diocletian at least brought some order, but things fell apart again after his death; Constantine (early 300s) reunited the empire but it began to fall apart basically as soon as he died.
If Disney or NetFlicked get ahold of it, it’ll be GLAADiator…
LMAAAO!
Yes – the movie centers on the time of Caracalla, Geta and Macrinus, and botches it all up as far as specifics, while doing a fairly good job of conveying the continuously conspiratorial, insurrectionist, and back-stabbing nature of Roman politics, as well as the abuse of its military.
Some of that is mentioned here…..
https://en.wikipedia.org/wiki/Macrinus
I agree with you.
Or Osatan made for him.
Alpha and Canncon have on a lawyer, a former Marine. He was a “…former Philadelphia Assistant District Attorney under Lynn Abraham, a former Assistant U.S. Attorney, District of New Mexico, and a former U.S. Marine machine-gunner.## He is Reeve Swainston. They discuss the Biden pardons and also whether the 2020 election could be over turned. Starts at 12:15
SITREP Ep. 98 – Political Drama, Pardons, and the FBI’s Double Standards
1:00 He talks about people he worked with at the front line level (O3s) in FBI. Those he is in contact with those are excited about Trump coming in.
An article written by Reeve:
## Reeve Swainston: A letter to my beloved Philadelphia, a once great city being ramshackled by surging crime rates and apathetic politicians alike
https://rumble.com/v60sv0z-sitrep-ep.-98-900-pm-et-.html
I bet there was a lot more going on than just napping. He was either being medicated or they were waiting for a med to wear off so he would be alert.
https://x.com/InvestigateJ6/status/1870287643386233261
https://x.com/i/status/1870277911309365387
Personal responsibility, accountability IS fundamentally required.
Punishment.Prevention.
Wow! I’m one of John Does 1-10,000! And I’m on audio yelling FU!!!
Wonder if I am.
Or whether I’d be in the range John Doe 10,001 through 100,000
Exactly! That 10K number is a bit low, IMO.
Careful. FIB might want you speak into the mike so they can compare voice prints 
for heaven’s sake….there’s welfare in every freaking bill they pass. that’s ridiculous!
FTA
The bulk of the Farm Bill is funding for food stamps, Sen. Ron Johnson (R-WI) said Thursday during an interview on Breitbart News Daily.
Sen. Johnson walked through some of the issues with the original 1,537-page continuing resolution (CR) negotiated by Speaker Johnson, which is full of pork. One of the stumbling blocks for some is the inclusion of the Farm Bill in the spending deal, but the senator said it is not what it seems.
“I guess, the leverage that is being thrown at us is, “We have to pass this because it has a Farm Bill in it, and it’s like, well, hold on,” host Mike Slater said, asking the senator to explain what that means.
“It’s a food stamp bill,” Johnson revealed. “80 percent of the Farm Bill is funding for food stamps, and Obama dramatically increased eligibility.”
“It used to be in prosperous times, maybe 6 percent of the population was on food stamps. Then [the] recessions, go up to 12 [percent] 13 [percent], pretty well stuck at that higher limit nowadays, because we pay people not to work,” Johnson said.
“Let’s be honest, we pay people not to work,” he said, noting that the U.S. welfare program is very generous.
“People don’t pay taxes on them [welfare benefits]. We have a huge transfer of wealth from working Americans to people who don’t work. And we’re a compassionate society. We want to help people who can’t help themselves. We want to help people help themselves, but we created a far too large dependent class. That’s got to end,” he said. “We need to get people off the couch. They’ve got to enter the workforce and grow our economy.”
Speaking to Breitbart News Daily that same day, Rep. Tom Tiffany (R-WI), a member of the House Freedom Caucus, also said the Farm Bill has “become largely a food stamp bill.”
“I mean, it is all about passing out the goodies, and therein lies the big concern with the Farm Bill for many of us is that as a result of being able to — the requirements to be able to qualify for food stamps are so loose and states do not enforce them well, so much of the money goes out fraudulently or goes out to people who really shouldn’t be getting the money,” he said.
“That’s the big problem with the Farm Bill. It isn’t so much helping farmers anymore. It’s become a food stamp program,” he added.
“I mean, there’s some good stuff in there for farmers, absolutely. But this is where the Democrats come back and say, ‘We want more money for the Farm Bill,’ because that’s the reason Democrats support the Farm Bill, not because of farmers, but because of food stamps,” Tiffany concluded.
https://www.breitbart.com/politics/2024/12/20/exclusive-ron-johnson-80-farm-bill-is-funding-food-stamps/
One thing I will remind people here about SNAP and those who frequent food pantries is that the majority of those who benefit are actually our more seasoned citizens on fixed incomes. These are older people who have retired, and those who are disabled. I have less a problem with that and the young widow with a few kids than I do the illegals milking the system. I suspect that’s what the additional funding is for, and that is infuriating.
YUP, it is for the illegals I am sure.
I take a friend to the food pantry every once in a while and there is NO CHECK on whether the person is telling the truth.
Also this is an ‘upscale’ mostly white county (82%.) And yet the people running it are Hispanic or speak Spanish. The people visiting to get goodies are black (11%) and Hispanic (13%) NOT WHITE ELDERLY (25%).
This food pantry hands out government purchased food as well as donated food.
Food pantries hand out whatever they can get their hands on.
we live in a small community–our town is a little over 1,000 people. and there is a food pantry there for those in need. farmers donate excessive produce and there’s a deer processor who regularly donates venison and other meats.
I have no problem with helping anyone in need. in fact every town around here has a pantry, a club like the Moose club that has Christmas parties for any child to attend and all sorts of community sponsored events all year round.
that’s what communities do.
food stamps for illegals is something else entirely. cut off the draw to come here–welfare, SS, free rent, free healthcare, free everything and they will stop coming.
Sorry, I was not clear. The connection was this food pantry gets FEDERAL FOOD BUT DOES NO CHECKING!
From other stuff I have seen, you get a lot of people working ‘under the table’ so they can stay on SNAP and such assistance.
This whole thing is a complicated mess. Years ago I was talking to a guy who built hand crafted musical instruments. I bought a Lap Harp from him. Anyway, back in the 1980s he was complaining that he could not AFFORD to hire anyone because they could make a lot more money sitting on their asses collecting welfare.
Since then, that has been my observation.
We have a local butcher who processes deer for the food pantries. It’s actually a big county program that thins out the deer population in the fall to keep them from overrunning all the people out in the far suburbs with expensive landscaping. And those are the people who object to the deer being culled. Go figure.
Assisting elderly, disabled, widow with kids and the like.
Illegals. Nothing.
Stuff SNAP can buy needs to be food only, exclude soda and candy. May already be that way. I have no idea.
It’s not that way.
It excludes prepared food…like the cooked stuff from the deli.
What we think of as “welfare” with unwed moms pumping out babies…was originally intended as a program for widows who had been left with children and of course the breadwinner now dead. That’s misfortune and it’s understandable that people would want there to be a program to cover it.
The problem is, the program doesn’t exclude children deliberately had out of wedlock.
No food program should exclude children, however they were born.
It should exclude soda, candy, junk food, and other crap, just like the WIC program does. As a matter of fact, I would like to see food stamps limited to certain foods. Beef, chicken, fish, or pork; fresh or frozen vegetables; rice, beans, flour, sugar, yeast, salt; fresh or frozen fruit; eggs, cheese, milk, butter, olive oil; etc.
If it’s food I agree.
I’m talking about the versions they simply hand mommy cash. There are literally entire communities where women are expected to support themselves by downloading fatherless kids.
Oh, yes, I am aware.
Though I am aware of people selling even their card benefits. They hand the card to someone else so they can buy food; in return they get some fraction of the money the guy saved.
So the WIC program proves that SNAP benefits can be tailored to appropriate standards.
So there’s no excuse for not having done it already.
I agree.
First we’d have to settle the current arguments over what healthy food is.
The WIC program does a pretty good job with it. It can be done.
And just like that…the dumber than dirt, drone hoax disappeared.
Yup. They must have found the missing whatever!
okay…I’ve read and heard some weird stuff, but this??? you gotta listen–even if it’s just for a chuckle
That was fun!
Now – to figure out which famous person I married! 
He says, “The most likely scenario here is that I’m just a crazy person and I’m delusional.” Yes, indeed. As for entertainment, the problem is that there are people who will latch onto it and run with it.
Yeah, this fucker knows exactly what he’s doing. Starting a new “conspiracy theory.” Honestly, can we just start kneecapping these assholes?
Diana/Melania would have to learn that new accent and never, ever slip. I didn’t even get the sense that the bone structure is the same between the two faces, either. It’s not like they just had to give Diana those rather oddly tilted eyes.
The easier explanation is that Barron simply takes after his father. Who he resembles far more than Diana Spencer.
Also Diana was born in 1961. Melania in 1970. Diana died in 1997, Melania’s modelling career started in the mid 1980s. She moved to Manhattan in 1996…a year too early to be Diana after a faked death.
but there were those matching dots on the faces…did you miss THAT????
/sarc
Fine with me.
I am confounded when people say someone looks “just like” someone else when they actually don’t, or else they don’t recognize that two photos are of the same person. IMO Barron resembles both of his parents.
I get you look just like [Cherokee relative…] all the time. They even haul out photos.
EACH DAY WE TAKE UP THE OFFENSIVE WEAPON OF THE WORD OF GOD – THE SWORD OF THE SPIRIT – ONE VERSE OPENS THE DOOR TO THE CONTEXT OF THE CHAPTER MESSAGE
Verse of the Day for Saturday, December 21, 2024
✟
“I am Alpha and Omega, the beginning and the ending, saith the Lord, which is, and which was, and which is to come, the Almighty.”
Revelation 1:8 (KJV)
Thank You, Jesus, for blessings received and prayers answered !!!
WE ARE FIGHTING A SPIRITUAL WAR OF GOOD VERSUS EVIL
PRAYING ON THE ARMOR OF GOD
Father God, I now follow your command to put on the full armor of God, because my battle is not against flesh and blood but against rulers, authorities, the powers of this dark world and against spiritual forces of evil in the unseen world.
I first pray on the Belt of Truth that it may be buckled around my waist, may I be centered and encircled by your truth dear Lord. Hem me inside all that is true and right, and may I be protected and held up by the truth of your living word, in my Lord Jesus name.
I pray on the Breastplate of righteousness, please protect my vital organs and my inner man, cover my integrity, my spirit, and my soul. Guard my heart for it is the wellspring of life, please strengthen and guard the most vulnerable places in my life with that which is right, good, and noble that I might not receive a fatal blow from the enemy, in my Lord Jesus name.
I pray on the Gospel Shoes of Peace. I choose to stand in the shoes of your good news, and on the firm foundation of my Lord and Savior Jesus Christ, the solid eternal rock. All other ground is sinking sand, I pray that I will not slip or fall, but that my feet would be firmly fitted on your lordship, my Lord Jesus. I choose to stand on you, so that the peace of God, which transcends all understanding will guard my heart and mind in Christ Jesus, the eternal Rock of Ages. I receive your holy peace now my Lord, from the sole of my feet to the crown of my head, in my Lord Jesus name.
I pray the Shield of Faith into my hand now. As I take up the shield of faith, I ask that you might extinguish every dart and arrow that is launched from the enemy to take me down spiritually, physically, mentally, emotionally, and every attempt of the enemy to destroy my joy. I ask that my faith in you would make it flame out. Extinguish every flaming arrow that would come against me, my life, my family, my home, or my ministry. May my faith always be out in front of me like a shield. Give me the courage to “faith my fears” by choosing to walk by faith and not by sight, in my Lord Jesus name.
I pray on the Helmet of Salvation, that you might protect my mind from the thoughts that can lead me astray. I choose to take every thought captive, and arrest all intentioned ideas and motives that would harm others, or distract me from your holy will for me. I submit every captured thought to the Lordship of my Lord Jesus Christ, and ask that you would imprison those thoughts that are not of you my Lord. Transform my mind and renew my thinking that I may think God thoughts, and have a sober mind that is focused on your glory. Please protect me from being double minded that I may allow my mind, I reject to live an earthly life, because I choose to live a holy one, governed by you My Lord Jesus, the prince of peace, please have my mind to be saturated with the holy mind of Christ, in my Lord Jesus name.
Finally, I take up the Sword of the Spirit which is the holy word of God, I pray this powerful offensive weapon into my hand, and ask that your holy word would be fitting for every encounter I face. As the enemy gets close to me, please give me the insight, wisdom, and skill to wield the word of God to drive away the enemy, in my Lord Jesus name.
May the enemy and his team flee from me, upon hearing the word of God spoken by the power and direction of the Holy Spirit. Give me the sword of the spirit to cut through the wiles of the devil, so that I may discern the schemes of the enemy when he is near.
With all kinds of prayers, supplication, and intercession I pray to you my Lord God as the one who fights my battles. Now that I’m in your holy powerful armor, I walk away covered and ready to face my day as you go before me, and please protect me in the midst of the spiritual warfare in this unseen world, in my Lord Jesus name.
Thank you my Lord, for the spiritual weapons of armor and prayer that you have given me. It is written no weapon formed against me shall prosper, and you will refute every tongue that accuses me.
Thank you Father God, my Lord Jesus and the Holy Spirit, that I am more than a conqueror in my Lord Jesus. I pray all of this in the mighty name of my Lord God and Savior Jesus Christ, Amen.
PLEASE PRAY FOR ABUSED, MISSING, AND TRAFFICKED CHILDREN
BE MY VOICE
JESUS LOVES THE LITTLE CHILDREN
CHILD NOT CHOICE
PLEASE PRAY FOR ONE ANOTHER
MAPA = MAKE AMERICA PRAY AGAIN
OUR PRAYER
We come to Your Altar on bended knee
In the name of Jesus – we pray to Thee
One of our loved ones is in peak peril
Demons they have her over a barrel
Another test will be taken real soon
Could sink hope or take her over the moon
By the Blood of the Lamb – we are healed
By His sacrifice – our fate – it was sealed
Protect her from all danger hurt or harm
We’re calling all Angels – set the alarm
Warring Angels by the dozens dispatched
Go after those demons – get them detached
Comfort Angels dispersed to quell the fear
Through Faith – we command fear disappear
Healing Angels anoint her with the oils
Cover her completely before she spoils
Relaying Angels with a message from God
Rest in His Arms – prepare to be awed
We take authority over our friend today
By the Power of the Spirit we humbly pray
We unite in our prayer – strengthen her
To guide those in charge of her to concur
Set all instruments so accurate they be
By the Power of the Spirit command them we
Take care in your analysis – through Hope
By your training and insight help her cope
God has given you the means to infer
A possible treatment that will deter
The failure of systems rightly attached
Your expertise surely cannot be matched
Let the Hand of God guide competent hands
To do what must be done – what He commands
As we lift her up to the Heaven on High
We give it all to You – and breathe a sigh
She is in good hands – the best there be
The Angels surround her – a sight to see
We lay our petition at the feet of Your Son
Whose victory over the cross He surely won
We know in control – You must ever be
We pray for a miracle for all to see
God can fix anything – He has the clout
The Power of God is awesome no doubt!
D01: 07/02/2019
Thank you, Duchess!
https://www.theqtree.com/2019/05/23/the-poetry-tree/#comment-1349373
Psalm 91. The most powerful prayer from the Bible. God’s protection, healing
#psalm91 #psalms #prayer
Pray Everyday
https://rumble.com/v57jz8d-psalm-91.the-most-powerful-prayer-from-the-bible.-gods-protection-healing-p.html
Sleep Well with Psalms. Psalm 91, Psalm 121, Psalm 3, Psalm 4, Psalm 139.
#faith #god #psalms
prayeveryday777
https://rumble.com/v57jvfg-sleep-well-with-psalms.-psalm-91-psalm-121-psalm-3-psalm-4-psalm-139.faith-.html
______________________________
HAVE A VERY BLESSED DAY !!!


Going to spend some time digesting this one, Steve. Thanks for the efforts you are putting in with these.
This was interesting. Looking forward to geology, here.
ditto
Sam’s purchase:
“Louisiana Brand” hotlinks. Made in California.
WTF.
Gosh, not even a Lousiana purchase… Aztlan links?
h/t Filly
“The fact that Kay Granger is unable to leave her nursing home to participate in the most important congressional vote of the year suggests she was already in visible decline when she ran for re-election in 2022.
A sad and humiliating way to end her political career. Sad that nobody cared enough to “take away the keys” before she reached this moment.
And a sad commentary on the congressional gerontocracy.”
—————–
“BREAKING: We got a tip from a Granger constituent who shared that the Congresswoman has been residing at a local memory care and assisted living home for some time. Why have the public and Ms. Granger’s constituents been left in the dark about her whereabouts and the nature of her absence?”
https://twitter.com/rdgarcia03/status/1870149666425188556
https://redstate.com/beckynoble/2024/12/20/more-tales-from-the-swamp-sitting-tx-congresswoman-found-living-at-assisted-living-home-n2183465
Shame:
WTF about the voters, that reelected the fraud. 
JAB JAB JAB JAB JAB
JAB JAB JAB JAB JAB
JAB JAB JAB JAB JAB
JAB JAB JAB JAB JAB
JAB JAB JAB JAB JAB
The JAB —
YES
YES
YES
YES
YES
For those who care:
Today is Day of Solstice.
Yeah, I guess so.
He has been atrocious this season. Must have something on his mind.
Tailor MAID indeed……
I just finally watched the video of McToon blowing up at Oakley. I get his anger. I wish he wouldn’t call Oakley’s “marks” idiots, but I understand. It’s rage-inducing having to deal with con artists.
It is the same thing we all went through trying to explain the Covid virus/vaxx hoax to people who fell for the lies. It’s frustrating when people have been brainwashed and when the brainwashers are confronted, they just come up with new lies for their victims to cling to.
It’s infuriating. I was so angry I had to stop talking about it to the sheep I know. Even though I was trying to save their lives, they just wouldn’t hear me.
This is a fair and good criticism.
But WHERE ARE THE GUNS, NATHAN!?!?
I’m guilty of calling marks idiots myself, on occasion. I try not to, but it’s hard.
Especially when they’re obstinate about it.
I found that video hilarious – particularly as MCToon was walking around the snowy lot with his phone, yammering at Oakley. It’s just ridiculous and bizarre! “YOU LIED!” LOL
It was funny.
Harrison
December 21, 2024 9:18 am
Corrupt Piglosi and her strange hubby once again in the news…
Nancy Pelosi and her husband appear to have used unreported $28 million in Covid pandemic grants to make their personal investments in a hotel profit, per RealClearInvestigations.
The two of its investors in the Auberge du Soleil, a five-star hillside hotel and spa.
The Auberge du Soleil investment, held for decades by Paul Pelosi, has rarely turned a significant profit, until 2021.
Then, Pelosi’s private holdings, such as the Auberge du Soleil resort, received upwards of $28 million in pandemic-related taxpayer funds, including the PPP, the COVID-19 Economic Injury Disaster Loan, and a special grant program for restaurants.
the Restaurant Revitalization Fund, one of the additional programs launched by the new round of pandemic spending, provided $5 million to the Auberge du Soleil in June 2021.
The first PPP loan, awarded the previous year, provided $2.9 million – helping the Pelosis earn millions on an investment that has rarely turned a significant profit, according to Nancy’s ethics disclosures
Hope Nanzi falls down some more steps.
Sorry. Not sorry.Would give many here a raging schadenböner.
Mob Princess Crime Family.
From five months ago, Will Duffy asking Eric Dubay (of the 200 proofs fame) why suddenly Dubay doesn’t want to go to Antarctica. Enough to know Dubay is a charlatan who needs CON MAN tattooed on his forehead.
H/T kyblue @ Sylvia’s
https://twitter.com/CynicalPublius/status/1870507537478676643
https://x.com/CynicalPublius/status/1870507537478676643
Cynical Publius
@CynicalPublius
To all you Doomsters convinced that rolling back the Neo-Marxist Democrat agenda is impossible, I want to offer you two words of encouragement:
Gun rights.
In the 1990s, the Second Amendment was on its deathbed. So-called “assault weapons” were banned, concealed carry permits were increasingly rare for ordinary citizens, “high capacity” magazines were the next target of the gun grabbers, Waco was legitimized as a necessary limit on unlawful gun ownership, and a national sensibility that only lunatics owned guns was taking hold.
We were well on the path to becoming Australia.
But a sophisticated, multi-level strategy by real conservatives, at the federal and state levels, in the courts and in Congress and in the statehouses, transformed all of that.
Heller.
McDonald.
Bruen.
The AR-15, once banned, is now the most prolific firearm in the USA.
More than half of US states have Constitutional carry laws.
Gun culture and the availability of reliable, accurate, reasonably-priced firearms have never been greater.
Women in the USA see their gun as the great equalizer against rapists and criminals.
Concealed carry classes are legion.
We may soon have reciprocal carry rights in all 50 states.
Where we stand in 2024 with respect to gun rights was INCONCEIVABLE in 1994. But here we are. We won, and we keep winning. Conservative ideas and policies CAN WIN. We CAN DEFEAT the tyranny of the Left. Gun rights show us the path.
So Doomsters, think about this, and realize the MAGA agenda is attainable, and will be attained soon. Be of good cheer.
We may soon have reciprocal carry rights in all 50 states.
^^^ We should.
Back in 2017 Eddie Munster and Turtle stopped it. Trump said he’d sign it.
Of course, with 2A as written, we shouldn’t need reciprocity.
We shouldn’t need permits.
“Constitutional Carry” often means a law that leaves all of the legal structure for the permit process in place. Can’t carry without a permit, yadda yadda. But then they stick one new sentence in that says a driver’s license and/or state ID (you can get an ID card that functions for purposes of identification but doesn’t license you to drive) for that state is considered a permit. Which means it doesn’t apply to people from out of state (which means it’s not true constitutional carry; your rights depend on where you live), and isn’t a true repeal of the requirement to have a permit.
A true constitutional carry statute would remove the ban on carrying without a permit, rip out the pages and pages of related statutes, rather than add a clause to say, “your driver’s license is a permit.” Removing a ban should shorten the legal code.
At least the last time I checked the Wyoming “Constitutional Carry” was like this. It applied only to Wyomingites.
[An argument can be made for leaving a voluntary permit process in place…for those who want to travel and would like reciprocity in states that still require a permit.]
29 DAYS, 23 hours, 28 minutes until our Once and Future President is restored to his rightful office.
Yes, we are now in the twenties. Less than 720 hours to go.
Not that I’m counting, mind you.
This is for DP.
At the Cathedral here, the organists put a label on a spare stop that said, “Clergy Eject.”
Does it have the same effect as a sforzando button?
Coothie
Pretty close.
Not forgetting “awful Clyde”
The ophicleide is not the weirdest stop on an organ.
The actual instrument, an unvalved ancestor to a tuba or euphonium (and sort of like a brass saxophone) is pretty rare these days, but it remains a semi-popular organ stop in large organs. It uses a metal reed and pipe and is frequently the loudest stop in a given instrument.
Yep. Most of my classmates at USC in the concert choir were church and choral majors, and double-major with organ was not uncommon, to the point that when we went on tour each semester for a week or two, every concert would also have an organ concert/recital with it…
I experienced Awful Clyde first hand… Durufle seemed to use it as a weapon…
N.B. Adolphe Sax was said to have been inspired by the ophicleide (emphasis on leid) when inventing the saxophone…
I have probably mentioned this anecdote before….
My maternal grandfather tuned and repaired pipe organs (when he wasn’t a theater projectionist and part-time MC).
One day, he took my uncle (who was just a kid) out on a job. While he was lying on his back across the pedalboard, poking at he bottom of the manuals with a voltmeter, my uncle wandered around inside the organ.
Then my grandfather bumped the sforzando button with his elbow. This turns on every pipe in the organ associated with a pressed key. Since he was laying across the pedalboard, that would have essentially been all of the white keys.
The position of the volume shutters would have no effect for someone actually inside the organ.
Obviously, my grandfather quickly figured it out, shut off the sforzando, and went running to find his kid — who, fortunately, was not permanently harmed or deaf. But my uncle held that incident against his dad for the entirety of his life.
As an odd point of interest, I actually saw that organ and the infamous sforzando button in San Diego, because my grandfather bought the organ when it was decommissioned and hauled it from West Virginia. Beautiful quartersawn oak. He gave some thought to cutting out the sforzando button and framing it for my uncle to hang on his wall, but he ended up hauling the organ back to the house in Parkersburg where he passed.
Needs to be in Latin.
In case anyone else can’t see it here, running it through Gab
I saw this over at Insty, and couldn’t recall if I’d seen it here before —
https://alexberenson.substack.com/p/why-do-so-many-people-have-ultra
The first comment is from a doctor and very interesting.
Missile attacks between Russian & Ukraine and Israel & Yemen are getting hard to track on twitter as far as what happened when to whom. Likely going to need Daniel Davis or Col McGregor to explain as they now seem to be a daily occurrence in the mean time we bring you this.
https://twitter.com/BentsCristin/status/1868051360429842674
In other interesting news there is this. We unfortunately do not know the context.
https://twitter.com/RussiaIsntEnemy/status/1870410933031297186
Gal blind.
Can’t read much else into it. Too rushed. Surprised at that.
Hoot hoot, still unpacking here. All is well. Have a great weekend everyone!!!
thanks for the giggle!
YW!
Good to “see” you. Hope all is well and life is good.
Good to see you too, TB and CC too! I am reading along but not contributing too much yet. Life is good. My great nephew is all grown with a daughter. He helped me get a vintage dining table home and was able to do all the carrying himself once we took the leaf out and folded down the sides. I think it is Duncan Phyfe and so are the 4 chairs I had already brought home. It only cost $75 at a small town antique shop and is in good shape. I just opened a box I’d marked as “fave nic nacs” and the first thing out of the box is a very old potato masher with a red wood handle. hehehe… I love taters but I use moderation. Kitties are adjusting fine. Brad is sitting as a centerpiece on the new dining table that already has a Christmas tablecloth on. Mia is on top of a medium size box watching outside where a birdhouse is at viewing-height in a crook of a very large tree. Across the gravel road, there are two horses in a nice-size pasture. I say hi to them when I walk out to get the mail. Love you all!!
“…very old potato masher with a red wood handle.” I have one but the handle is green. It was OLD when I was a grade schooler.
It was OLD when I was a grade schooler.
I use a potato ricer, myself. Has a fluffier result.
Mine is similar to
I did not say I actually USED it. 
If I do potatoes it is baked or very rarely fried with onions. (My house guest wanted them.)
I might of glossed over that or I would of asked if it was some like this…

That one might be made of German chocolate…
These aren’t though.

Sounds about perfect. Have a very Merry Christmas now that you are finally Home again!
Love to you too, Barb. Glad you are settling in and sound so happy. This was a great move for you.
And they have to Peru(se) the situation
Happy (un)Boxing Day
Apparently Flat Earth Dave’s app is still the most insecure piece of crapware out there:
Not only is Flat Earth Dave a scammer, he’s not content to take your money, he’ll dox you too.
Only idgits did not know this would be how a war between Russia and Ukraine would turn out. All of it has been to benefit the nazis using human lives for money and a sacrifice to Satan.
Think about our own elected officials voting for this destruction and using tax payer funds to do it. Uniparty and the IC screwing all of us over.
https://www.theamericanconservative.com/ukraine-has-had-its-fill/
H/T kyblue @ Sylvia’s
https://twitter.com/JoeLang51440671/status/1870503777549336908
https://x.com/JoeLang51440671/status/1870503777549336908
JoeLange
@JoeLang51440671
Don’t miss what happened.
Trump, Johnson and Elon, trapped Congress.
I think it worked perfectly.
Here’s what Trump just accomplished:
Trump got the funding he needed for the important things, so he can hit the ground running on Jan 20.
He FORCED Congress to help two groups of Americans devastated in the hurricanes that were getting almost no assistance because all the money was spent on illegals. (Hurricane victims and farmers)
He FORCED the “process” out into the sunlight and allowed the American people to “read” the bill BEFORE it was voted on.
Why is that so important?
We all witnessed what happened to that 1547 page bill.
It got torn apart on X and everywhere else on social media.
The American people rose up and killed that bill.
The American people are taking back their government. Trump is “teaching” them to stand up and hold these “representatives” to account.
In the past, the Speaker would have dropped that 1547 page CR on Friday and forced Congress to vote on it without reading it.
This time, the American people got to read it first.
You saw what happened.
In the past, Congress wouldn’t have cared that the American people were outraged by a last minute 1547 page boondoggle. They would have passed it anyway, without fear.
But everything has changed.
They all saw the election results.
They no longer control X.
X is the greatest weapon in the narrative war and the American people now control it.
Their greatest fear has become reality.
A good government, is a government that fears the American people’s wrath.
What else did Trump accomplish?
He set the “standard” going forward of how this “process” is going to work from now on.
All bills in the House are now going to be slimmed down version for every bill.
We are going to get votes on single topics.
And the American people are going to be able to view and decide whether they approve or not, BEFORE it gets voted on.
Every member of Congress is going to personally hear from their constituents BEFORE they vote.
All of these “wins” are safeguards that weren’t in place BEFORE Johnson ever became Speaker.
Give him some credit.
This was Trump’s plan from the beginning.
Trump just “RESET” how the House does business going forward and most people are completely missing it.
Term Limits and Page Limits…
and Salary Limits…
12.21.24: SO much WINNING, TRUMP has THEM where he wants THEM, The TIDE is TURNING, PRAY!
And We Know
https://rumble.com/v61jyaz-12.21.24-so-much-winning-trump-has-them-where-he-wants-them-the-tide-is-tur.html
Tucker Carlson tells me there is something “profoundly wrong” with Speaker Mike Johnson, and calls his support of other countries over the U.S. “a kind of treason.”
“I watched him make the number one priority of his speakership funding Ukraine”
Full interview coming soon.
https://twitter.com/eduneret/status/1870284002755850286
Yup. Something very weird happens to congressional leaders. It’s like they get mind-controlled.
EVENING PRAYERS
Prayer Of Thanksgiving In The Evening
Praise Your holy name Heavenly Father, for granting yet another day in my life and for being with me every step of the way. Thank You for the many blessings that You have provided and the love and fellowship that I have with the friends and family that in Your grace You have placed in my life.
My heart is so thankful for all the many blessings that I enjoy day by day, and today I am once again reminded that Your mercies are new every morning and Your faithfulness endures from generation to generation.
Thank You, that I have been brought into Your family and have been made a child of God and a citizen of heaven. Words cannot express my love and devotion to You Lord
I pray that You would watch over me as I rest tonight, and that You would give me a restful night’s sleep so that I may wake up in the morning refreshed in body and spirit and ready to do Your will. Guard all those that I love and may we all grow in grace and in a knowledge of the Lord Jesus Christ in the days that lie ahead. This I ask in His precious name,
Amen.
Source: https://prayer.knowing-jesus.com/Evening-Prayers
_____________________________
Prayer Of Reflection On The Past Day
Loving Lord, as the day is coming to an end, I want to thank You for being with me in all that has taken place today. I also want to lay the whole day before You, asking that you would show me if there is anything that I have done to hurt or harm another person unknowingly, or if I have done anything that is displeasing in Your sight, or quenched the work of the Spirit in me, so that I may turn away from such things in the days that lie ahead.
Lord, I desire to do Your will in all things. I pray that You would cleanse me of any wrong thoughts or attitudes that may have surfaced in my heart today. Wash me in Your cleansing flood, I pray.
Thank You, that You are a God who forgives our transgressions when we are willing to confess them to You, knowing that such cleansing before You immediately draws us back into sweet fellowship with Yourself.
Give me a good night’s rest I pray, and may I rest quietly in Your loving arms in the knowledge that in Christ, I am eternally secure, due to Your amazing grace, for which I praise You. In Jesus’ name,
Amen.
Source: https://prayer.knowing-jesus.com/Evening-Prayers
______________________________
Evening Prayer For Forgiveness
Heavenly Father, thank You for bringing me through this day and Lord, forgive me for the times when I have wandered outside Your best will for me, instead of trusting You implicitly.
Thank You, that You are such a gracious Shepherd to me and that You come and rescue me even when I lose my way and stray from the path that You have laid out for me.
As I look back over today, I know Lord that there were things that I should have said and done differently, and times when I reacted in a manner that was not honouring Your holy name. Forgive me I pray, but thank You, Father, that You always faithfully prepared to gently bring me back to Yourself.
Give me a good night’s sleep I pray, knowing that there is no condemnation because I am in Christ, and may I wake up in the morning refreshed and ready to do Your will. In Jesus’ name I pray,
Amen.
Source: https://prayer.knowing-jesus.com/Evening-Prayers
Base Spike Detox. ~73 seconds. McCoullough.
Safe and effective not unsafe and defective like a certain (Jab).
https://twitter.com/CartlandDavid/status/1870529698826215766
Spoiler.
Similar information commonly posted QTree, including today.
Do not forget the Vit C & D & B12
Not to mention zinc, selenium & magnesium
Fortunately all of those are already on my list, which includes a third of the alphabet and a quarter of the periodic table.
 only 1/3 and 1/4?? Did you forget the Arsenic?
only 1/3 and 1/4?? Did you forget the Arsenic? 
(Turns out we, or at least some mammals need arsenic)
I must confess to having difficulty locating astatine supplements. (Yeah, I know you said “arsenic.”)
I know a lot of people who have severe arsenic deficiencies at least as far as societal health is concerned.
That article by E.M. Smith (Chiefio) was a bit of a surprise.
Not sure you caught what I was driving at in the second paragraph.
I got it…jab ’em & slab ’em, as it were; they won’t be missed!
OOPS, sorry about that. I thought it said 12 grams not “… human arsenic requirement is 12 mcg/day…”


Nope. I have no idea what chiefio article you’re referencing.
I am saying that someone like Soros needs a LOT MORE arsenic in his diet to ensure the health not of himself but of society.
Click on the word Arsenic.
And I am sure a daily dose of 12 grams would be lethal.
Yeah, a six order of magnitude error is trivial.
Think we could convince them they really needed that amount?
Or there is the old horse traders trick. Feed a tiny bit of arsenic, increasing the daily dose slowly. It makes you eat and gain weight. (Nice fat shiny OLD horses) Then quit. The victim stops eating their head off, loses the weight and the arsenic stored in the body fat is released.
AND old lace
Starting out on vitamin C and a couple prunes…not a good combination.
I’m off for the week. I just can’t do it. Hate to miss Christmas, but there’s nothing for it.
Prunes???
Get some decent rest and please get well.
Yeah, my system(s) are massively out of whack.
If you are taking more zinc than you are accustomed to, it can cause this kind of issue.
I know it’s basic, but make sure you are drinking plenty of water.
I hope you feel better soon.
Bannon. Gaetz ought to take the Oath AND get back in the fight. D U H !
To hell with yammering talking head on OAN.
Bannon: @mattgaetz needs to know the people have his back. Do we care about the Ethics Committee? No. Do we want Matt back? Yes. He must return in Jan, take the oath, and join the fight. We don’t retreat—we fix bayonets and advance.
https://twitter.com/Bannons_WarRoom/status/1870542198191825048
In an information vacuum this sounds good.
I have no idea whether Trump has other plans for Gaetz, that might be better.
OAN has very limited viewership so he’d be useless there.
OAN being throttled was my thought as well.
I do think Gaetz and others are being held for later deployment.
Agree. If Trump has a place for Gaetz, that’s the priority.
Bannon again.
Me. Gaetz needs ti get back in the House AND be the worst nightmare for Johnson, AND Uniparty.
Steve Bannon fires up the audience about @mattgaetz ’s savage tweet: Gaetz warns the establishment that if they keep playing games with the ethics committee, he’s coming back on Jan 3rd to expose who slept with who—every intern, every secretary, every page. Gaetz isn’t backing down, and DC should be terrified.
https://twitter.com/Bannons_WarRoom/status/1870537172417437920
https:/twitter.com/Shawn_Farash/status/1869895495214325910
https://x.com/Shawn_Farash/status/1869895495214325910
One minute of festive Christmas Cheer!
See new posts
Conversation
Shawn Farash
@Shawn_Farash
TRUMP SINGS: “WALKING IN A MAGA WONDERLAND” https://abs-0.twimg.com/emoji/v2/svg/1f3b6.svghttps://abs-0.twimg.com/emoji/v2/svg/1f384.svg
Steve Loves his posts earning these participation trophies!!!

I just “awarded” him his 300 “honor” LOL
Something VERY STRANGE is going on in DC. First Camel-Uh cancels her Vegas vacay, and Joe and Jill rush home from Delaware. Now this:
“Joe’s taking another vacation at taxpayer expense before he leaves office. He’s loading up Air Force One and kicking off his new year in Rome, Italy! Let the grift begin.
The president allegedly sprung this three-day trip on his White House staff, codenamed “President Actual,” at the last minute. They’ve ordered Air Force One to get gassed up before the Jan. 9 start and told the ambassador to vacate the Villa Taverna, because he’s staying until Jan. 12.
Actually, we don’t really know where Joe’s staying, but we have that in common with Joe. He often doesn’t know where he’s going or where he is. Indeed, he routinely has no idea what day it is, what he’s doing, what to say, and with whom he’s saying it.”
https://pjmedia.com/victoria-taft/2024/12/21/joes-last-grift-n4935338
Just as long as it is NOT New Zealand!
THE CASE FOR NUCLEAR WAR
Non-stop within range. In-flight refuel.
Taco Jill is collecting on more IOUs.
Maggot has no clue where he is, if he’ll be traveling.
Naps, ice cream and sniffin, is Maggot’s life.
And just what he’s sniffin, depends.
Comma needs to go after “what”…
Lol.
Here’s another take on the “volte-face” across the board performed by Mike Johnson:
https://x.com/TonySeruga/status/1870145753567637606
Spoiler: Has to do with Kevin McCarthy having a certain “meeting”; with Johnson meeting with SCIF; with a “relationship” with an underage m*nor. Leads up to the “volte-face” regarding “MAGA and America First.”
To clarify…this is the “volte-face” back after Johnson was elected.
Not the recent one on the continuing resolution.
Looks as though Johnson’s johnson got him in trouble.
Are You Being Served restaurant scene:
Miss Braums, looking at Mrs. Slocum “We’ll have two John Thomases”
Captain Peacock with a quizzical brow “I think you mean two Tom Collines”
ahem…
Nasty the Pig is also out of country. If Soros & Gates leave, I will really get worried
CollinesCollinses…sighSteveInCO
You’re correct. The SCIF meeting with Johnson was the “start-off.”
I heard it was the intel community that had the meeting with Johnson.
Yes. I think they flipped him with something, but not blackmail. I think he was convinced that he had to “help” in some fashion. That’s his weakness – a “duty to help”. They used his weakness to get him.
Probably highly classified.
The alternate hypothesis: There is actually a damned good (but highly classified) reason to support Ukraine no matter what. In other words, they “got to him” with a legit reason to change his mind.
A reason good enough to sacrifice the lives of the young men of Ukraine so that the next generation will not have Ukrainian fathers? Seems like a damned reason, indeed.
I was thinking along the lines of convincing evidence that Putin is indeed trying to reassemble the Eastern bloc.
What I am driving at here is, we’ve been assuming that there are only corrupt motives for supporting Ukraine, but basically everyone gets sucked into it. What if we have good reason to want Russia to lose that war, but it’s a classified reason?
Both situations would look the same to us on the outside.
I would assume that Putin has been trying to reassemble the Soviet Union since he first assumed office. I just don’t think that can justify the extermination of Ukrainians as a people, which was an easily foreseeable outcome of feeding their military-age males into a meat-grinder against the Russians.
Instead, it looks like a “let’s you and him fight” deal where our “allies” are facing genocide at our instigation.
And, no, I am not a long-lost descendant of Neville Chamberlain, or such a fan of Russia that I’d blithely grant them anything they wish. But the seeds of this fiasco were sown long ago — mainly with the idea of “flipping” Warsaw Pact nations into NATO based on their color-revolutioned “elites” instead of the will of their people.
I’m just furious that our nation has been turned into the patsies of this deal, providing Ukrainians transportation service into their version of Katyn Forest — but an order of magnitude larger.
You know what I don’t understand?
Why would anybody with a skeleton of this magnitude hiding in their closet go into public life? Are they fucking suicidal?
My read is that it’s not pedo. Read the full Daily Mail piece. I think Mike Johnson and his wife are actual Christians, who decided to provide what normalcy they could to a troubled kid, and for whatever weird reasons, God let them do it without being burned by it.
I think the Ukraine 180 that Johnson did is due to something else, and this is chaff to throw us off the trail.
In other words, it’s not a real skeleton. They’re fooling us on this, IMO.
Well, yes, I tend to agree. We have no evidence this is true. But we agree there IS leverage, big enough to make him 180. So my comment still stands.
SteveInCO
Thank you for the opener today!
IMO, the Flerfers, along with those who still insist that the COVID-19 bioweapon injectables are “safe and effective”, must be cut from the same cloth.
Looking forward to the Geology series.
In one way–not sure if it’s superficial–they are mirror images.
Flat Earth is actual science denial; they’re attacking the consensus.
The slabjab supporters are upholding the consensus. The issue there is the consensus was artificial rather than organic.
Indeed. Gravity and modern astronomy had to fight their way into acceptance.
PRECISELY, my perspective…
ht Truth
AAAAAAAMEN!
No bullshit!
Just the bull.
Love it!
Can only hope Speaker Johnson gets gored after listening to this dribble.
https://twitter.com/GuntherEagleman/status/1870590419312243150
Yup someone has his balls in a vice IMO.
https://twitter.com/para59r/status/1870683903234658407
On the dot via late reading catch up…Merry Christmas